Leveraging Quantum Optimal Control Theory to Enhance Photon-Based Information Transfer  

Study conducted by Prof. Guofeng ZHANG and his research team

Quantum technology is rapidly transitioning from theoretical marvel to practical tool, promising revolutionary advances in computing, communication and sensing. At the heart of this transition lies the quantum network—a system where distant quantum processors, or stationary qubits, are connected to share information. For these networks to function, information must be transmitted between nodes. This is where the flying qubit comes in.

Imagine a flying qubit as a quantum parcel. Its contents are fragile quantum states—like the "0" and "1" of a classical bit, but existing in superposition. This parcel is not carried by a truck, but by a single particle of light (a photon) travelling down a waveguide, akin to a fibre-optic cable for quantum data. For the recipient to successfully open the parcel and retrieve its pristine quantum information, the package must arrive not only with its contents intact but also in a very specific shape and form. The "shape" here refers to the photon's temporal profile—how its probability of being detected is distributed in the time domain. Mismatched shapes lead to lost or corrupted quantum information, crippling network efficiency.

In a paper published in Physical Review Applied [1], Prof. Guofeng ZHANG, Professor of the Department of Applied Mathematics at The Hong Kong Polytechnic University, and his research team explore a groundbreaking approach to this critical shaping problem. The featured research introduces Quantum Optimal Control Theory (QOCT) to the domain of flying qubits. By treating the shaping process as an optimal control problem, the authors demonstrate how to design control pulses that mitigate the imperfections of real-world hardware, paving the way for more reliable and high-fidelity quantum networks.

Generating a flying qubit typically involves an emitter (e.g., a superconducting transmon qubit) that couples to a waveguide (Figure 1). The emitter is prepared in a desired quantum state. By manipulating the coupler—the link between the emitter and the waveguide—this state is mapped onto a photon and released. An ideal system would use a perfect two-level emitter and a coupler whose strength can be tuned perfectly and instantly to sculpt any desired photon shape.

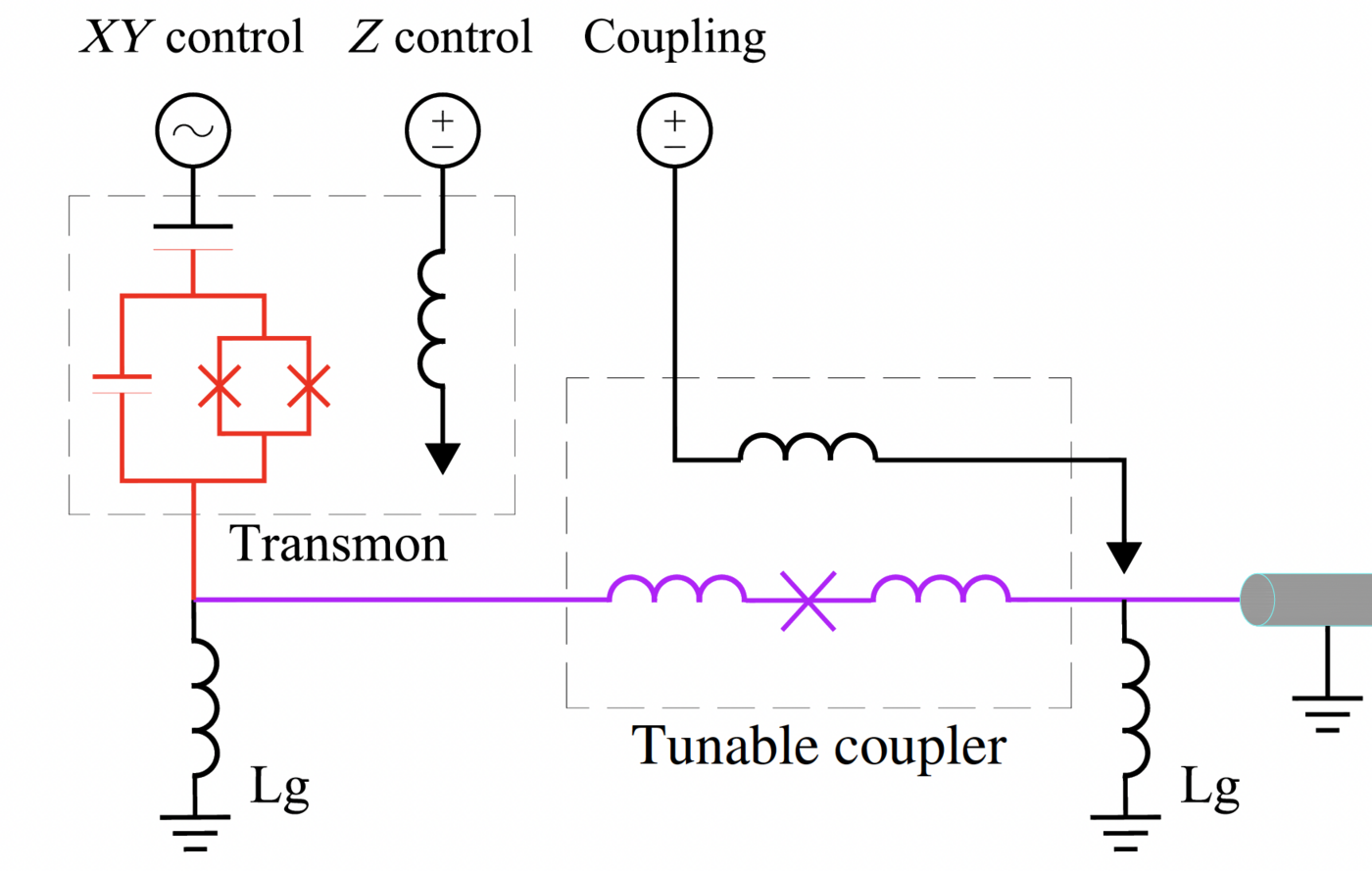
Figure 1. Schematic of a microwave flying-qubit emitter implemented by a transmon qubit. The emitter is inductively coupled to a transmission-line waveguide through a tunable gmon coupler. The transmon qubit is frequency tunable by the Z control, and its state can be coherently manipulated by the XY microwave driving field.

Reality, however, imposes harsh nonidealities:

1.  Anharmonic Emitters: Practical emitters like transmon qubits are not perfect two-level systems. They possess higher energy levels, leading to level leakage, where the quantum state leaks into these non-computational states during control operations.

2.  Limited Tunable Couplers: Real couplers have finite tuning ranges. They cannot be turned completely "off," leading to unwanted photon leakage (premature emission), nor can they reach infinitely strong "on" states, limiting the ability to generate shapes with sharp features (like exponentially rising temporal profiles).

3. Coherent Control Complications: Applying a microwave driving field to the emitter can help with state preparation, but it often triggers the emission of multiple photons, polluting the desired single-photon flying qubit state.

The core challenge is to choreograph the dance between the emitter's internal dynamics (controlled by microwave drives) and its release mechanism (controlled by the tunable coupler) to produce a perfectly shaped single photon, all while battling these intrinsic hardware limitations.

The research team established a comprehensive mathematical framework to tackle this challenge. The system is modeled using an effective non-unitary Schrödinger equation that captures the dynamics of the anharmonic emitter under the influence of two key time-dependent controls:

i. Coherent Control (u(t)): A complex microwave pulse driving the emitter.

ii. Incoherent Control (γ(t)): The tunable coupling strength between the emitter and the waveguide.

From this model, the temporal shape of the emitted single-photon component, `ξ(t)’, can be calculated. The power of QOCT is then harnessed by defining precise objective functionals—mathematical expressions quantifying the task's success—and finding the control sequences that minimise them. Subsequently, a gradient-descent algorithm is employed to efficiently navigate the complex landscape of these functionals and find high-fidelity control pulses, subject to practical constraints such as bandwidth limits and smoothness requirements.

Numerical simulations for a transmon-based system yielded critical insights into the roles of coherent and incoherent control.

1. The Limited Power of Coherent Control Alone

When the coupler has a fixed strength, coherent control u(t) shows some capability for shaping. It performs best for naturally decaying shapes but struggles severely with rising or symmetric shapes. For the state-transfer task, conditional emission largely fails; the photon shape is almost independent of the emitter's initial state, rendering it useless for quantum information transfer. The conclusion is clear: coherent control alone is insufficient for high-quality flying-qubit shaping.

2. Coherent Control as a Vital Complement

The paradigm shifts when a tunable—but limited—coupler is introduced. For challenging shapes like the exponentially rising photon, an ideal coupler would require infinite strength, which is impossible. A realistic cutoff scheme performs poorly (Figure 2a). However, when an optimised u(t) is added alongside this limited γ(t), performance improves dramatically (error drops from 0.112 to 0.038). Joint optimisation of both controls yields the best result (Figure 2a, error 0.028). The coherent control actively compensates in the time regions where the coupler's tunability fails (Figure 2c).

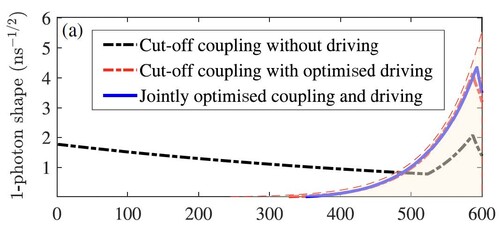
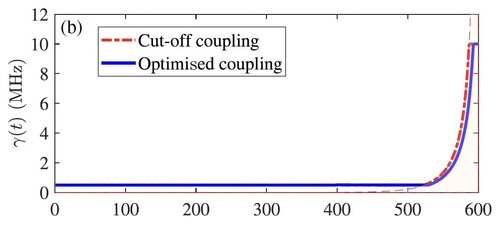
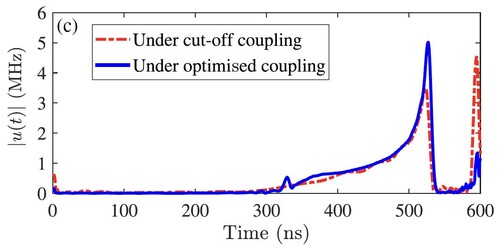
Figure 2. Fitting results of exponentially rising shape flying qubits
(a) Single-photon pulse shapes
(b) Corresponding tunable coupling function 
(c) Amplitude of the control pulses

This synergy is starkly evident in the state-transfer task (Table 1). A fixed coupler with coherent control fails completely (Total Error: 0.8127). A limited tunable coupler alone performs better but is still inaccurate (Error: 0.3435). Their combination, through joint optimisation, reduces the error by nearly an order of magnitude (Error: 0.0968). Coherent control is not the star, but an essential supporting actor that unlocks the full potential of a tunability-limited coupler.

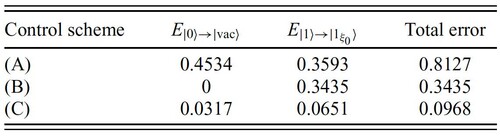
Table 1. Error under state-transfer control schemes
(A) Fixed coupling with tunable coherent control
(B) Tunable coupling without coherent control 
(C) Jointly optimised coupling and coherent control

The optimised controls designed were shown to outperform standard Gaussian and DRAG pulses significantly (Figure 3). They successfully suppress both level leakage (population in states |2⟩, |3⟩, etc.) and photon leakage (unwanted early emission), achieving fidelities of over 99.4% (Figure 4). This demonstrates QOCT's effectiveness in managing the specific imperfections of real-life hardware.

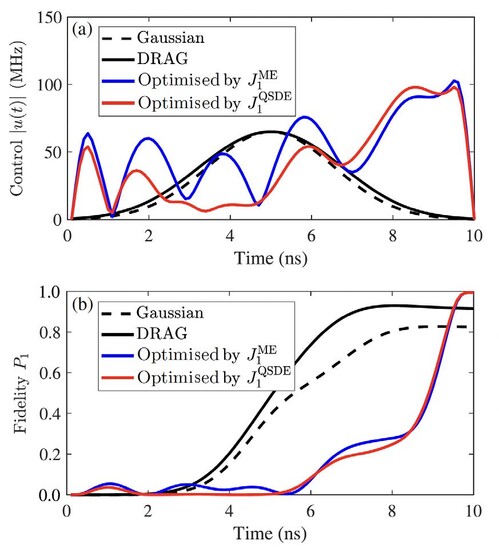
Figure 3. (a) Amplitude of the Gaussian π-pulse, the DRAG pulse and the optimised control pulses subject to objective functionals.
(b) Fidelity of the transmon qubit in the target state |1⟩, during the control process.

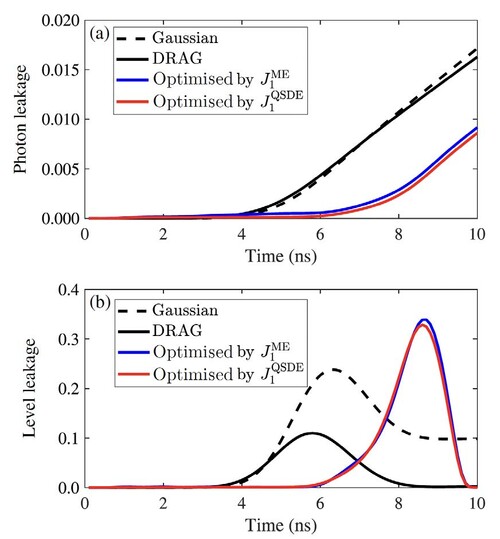
Figure 4. (a) Photon leakage 1 − |ξ ⁽⁰⁾|² and (b) level leakage (total population P₂ + P₃ + P₄ of noncomputational states |2⟩, |3⟩, and |4⟩) during state preparation.

This work represents a significant advance in the control of quantum light-matter interfaces, with the following key achievements:

1.  Pioneering Application of QOCT: This research successfully adapts Quantum Optimal Control Theory—a powerful tool in the manipulation of stationary qubits—to the distinct domain of flying qubits, establishing a novel design paradigm for quantum photonics.

2.  Holistic Handling of Real-World Imperfections: The framework simultaneously addresses major nonidealities prevalent in superconducting quantum platforms: the anharmonicity of transmon emitters (level leakage) and the restricted tuning range of practical couplers (photon leakage).

3.  Clarified Control Roles: The study provides a definitive analysis of the separate and joint capabilities of coherent (u(t)) and incoherent (γ(t)) controls. It conclusively shows that while a tunable coupler is fundamental for shaping, coherent control is a critical complementary tool for mitigating tunability limits.

4.  Provision of a Flexible and Practical Framework: The methodology is not limited to specific hardware. The gradient-based optimisation, complete with derived formulas (Appendix A), offers a systematic and adaptable approach that can be extended to other emitter types and multiple waveguides, and integrated with advanced optimisation or robust control techniques.

The introduced framework opens several exciting avenues for future research. Immediate next steps include extending the control design to more complex tasks, such as the generation of entangled pairs of flying qubits for distributed quantum protocols or the capture and conversion of flying qubits at a receiving node. Furthermore, the ultimate goal is to design flying-qubit-mediated remote quantum gates, enabling direct quantum logic operations between two distant stationary qubits without prior entanglement distribution.

In conclusion, the efficient control of flying qubits is a cornerstone for the realisation of functional quantum networks. By translating the shaping problem into an optimal control challenge, this work provides a powerful and systematic engineering toolkit. It moves beyond idealised models to deliver solutions for today’s imperfect devices, marking a crucial step from laboratory experiments toward scalable and reliable quantum information technology. The synergy between intelligent control design and advancing hardware will ultimately shape the future of quantum connectivity.

Prof. Zhang is a leading member of the Research Institute for Quantum Technology at The Hong Kong Polytechnic University. His research interests include quantum information, quantum control, quantum algorithms and tensor computation. He is an Associate Editor of IET Control Theory and Applications and Journal of Control and Decision and was the Lead Guest Editor for the Special Issue on Quantum Control and Quantum Machine Learning for the Journal of The Franklin Institute. He was the General Chair of the 2025 IEEE International Conference on Quantum Control, Computing and Learning (IEEE qCCL2025), 25 – 28 June 2025, Hong Kong.

[1] Dong, X., Cao, X., Li, W-L., Zhang, G., Peng, Z. & Wu, R-B. (2025). Quantum Optimal Control Theory for the Shaping of Flying Qubits, Physical Review Applied 23, 044045. https://doi.org/10.1103/PhysRevApplied.23.044045

Prof. Guofeng ZHANG Professor, Department of Applied Mathematics