High Speed Flow 

The space-time conservation element and solution element (CE/SE) method is a unique computational fluid dynamics (CFD) algorithm. It differs substantially in both concept and methodology from conventional method. The space and time are treated unified and the discrete scheme is derived from the original space-time integral form of the governing conservation laws. It can be proved that the discrete scheme satisfies both local and global flux conservations in space and time. Our group has implemented CE/SE method on general hybrid meshes (consisting of both triangular and quadrilateral elements) and extended it to high-order versions including third and fourth order. In our recent efforts, a family of upwind CE/SE schemes is also developed to further improve its accuracy and robustness. We also apply our in-house CE/SE in the research of: (1) hypersonic non-equilibrium flows; (2) detonation waves; and (3) two-phase compressible flows.

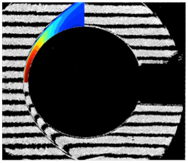(a)  Nitrogen flow                            (b) Air flow                              (c) CO2 flow

Figure 1. Hypervelocity non-equilibrium flows over spheres 

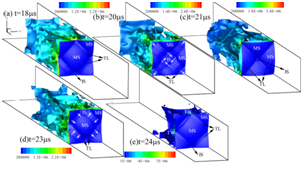
Figure 2. 3D detonation propagation in a rectangular duct

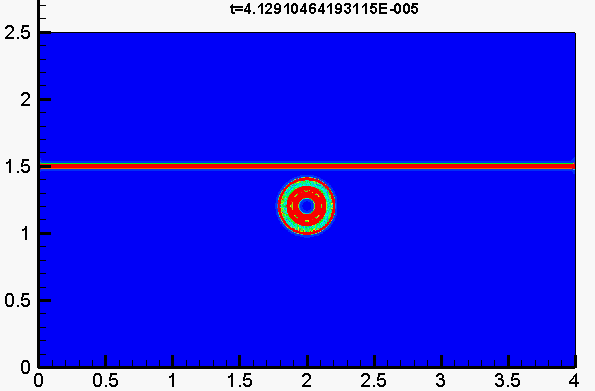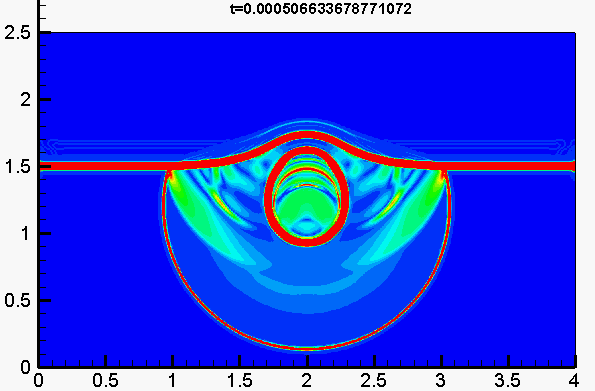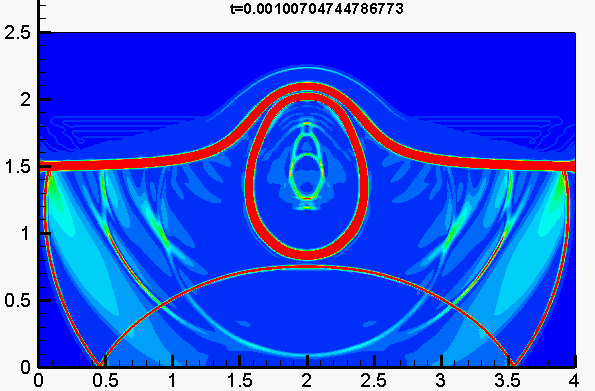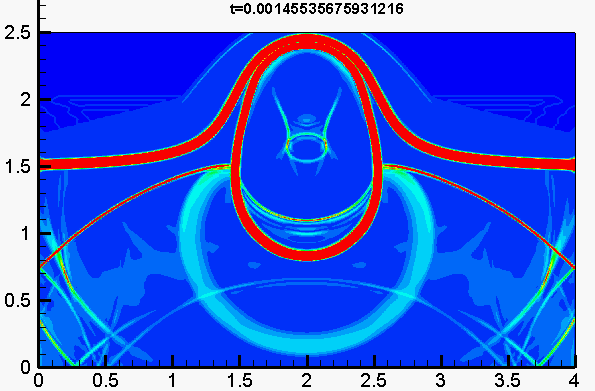
Underwater explosion

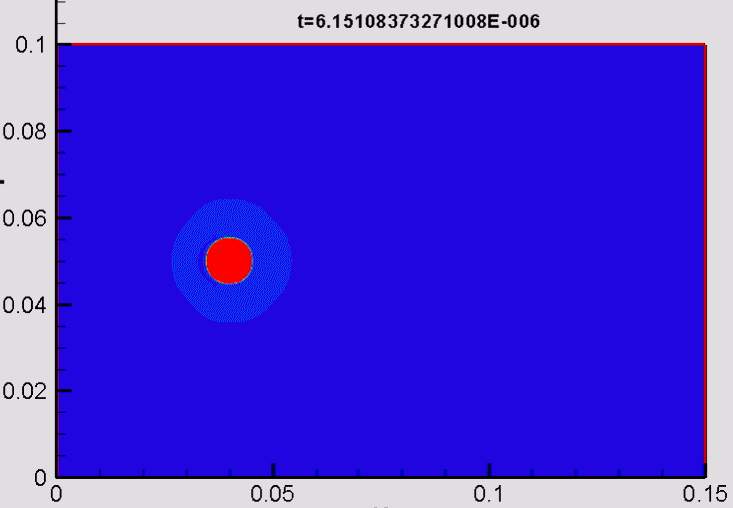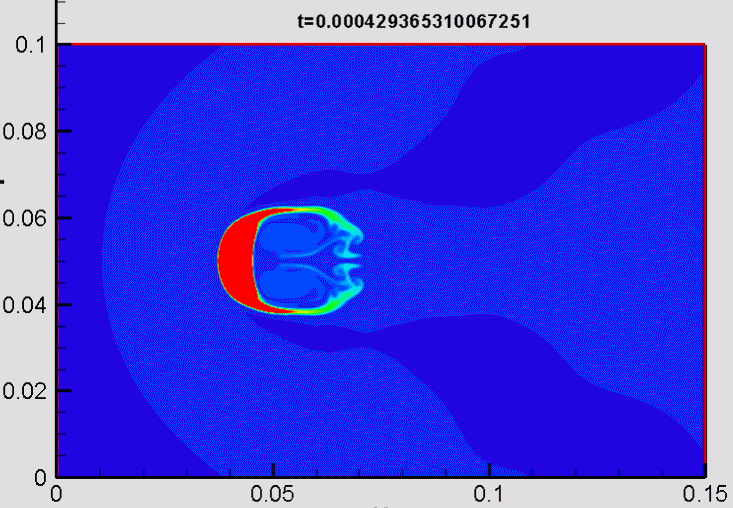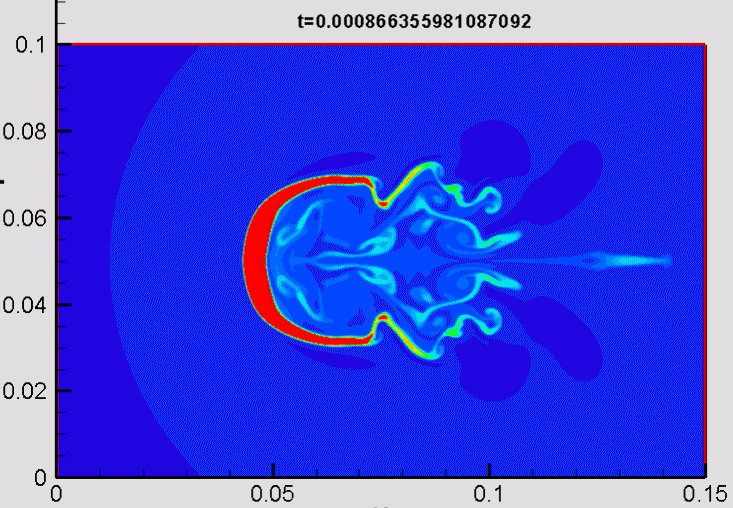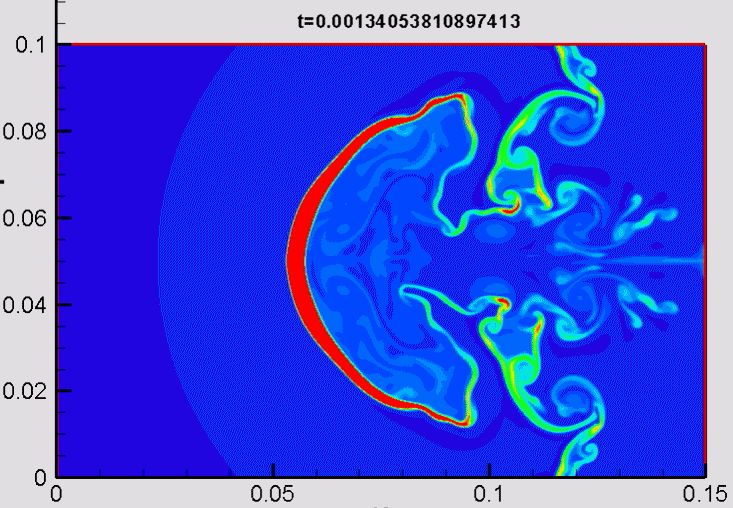
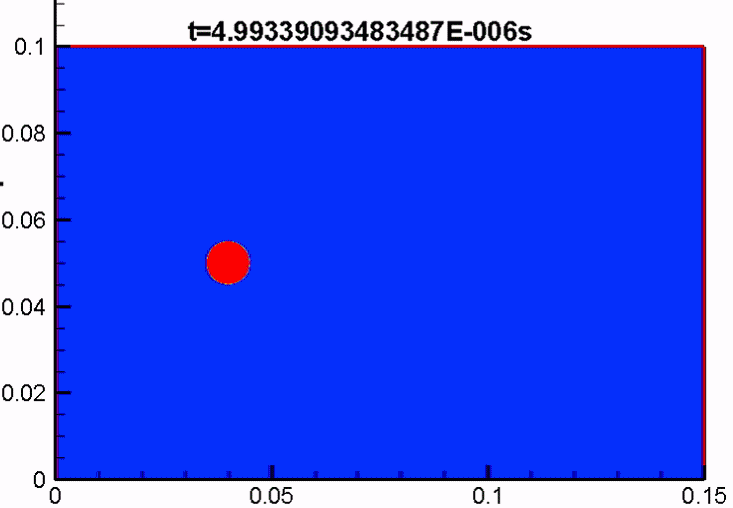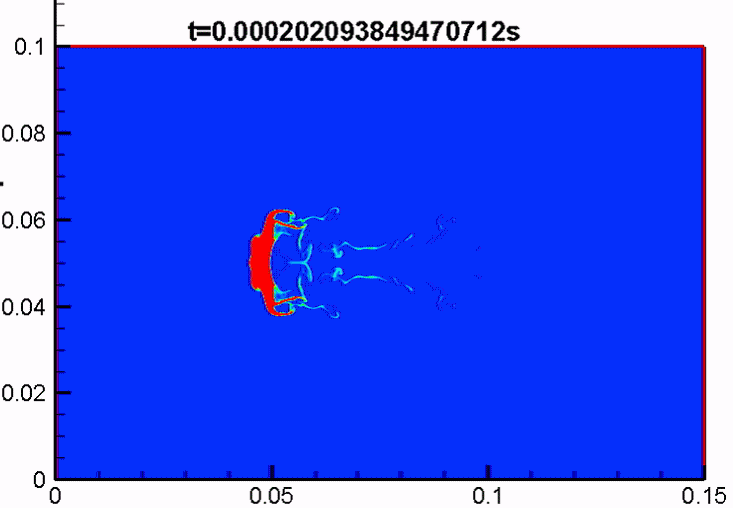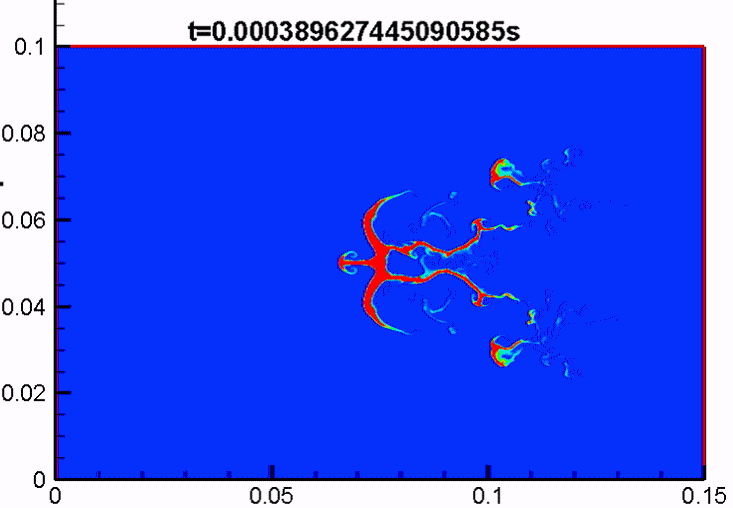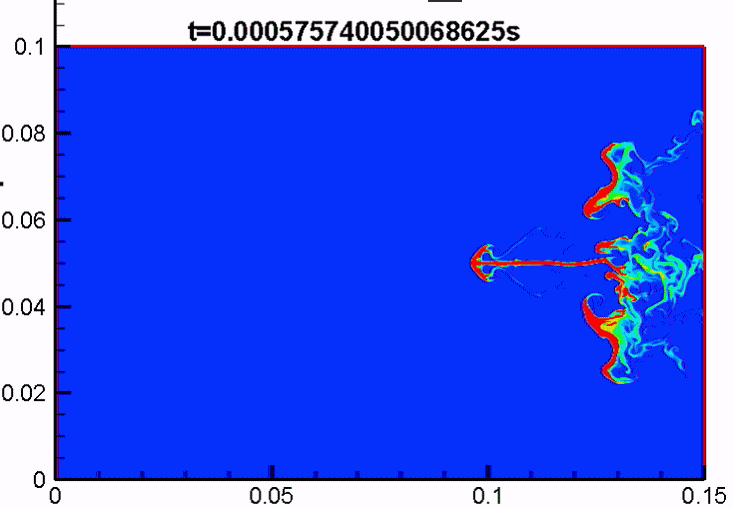
Shock/droplet interaction

The disagreement between numerical simulated detonation cell size (Figure 1.) and the experimental measured data has been recognized a long-lasting problem under resolved. In present study, our group developed an averaged temperature model in order to involve the impact of vibrational non-equilibrium on the prediction of detonation cell size. This distinct conception preliminarily succeeds in narrowing the disparity between numerical results and experimental observation (Figure 2.). Compared to the measured cell size provided in literature, the disparity in cell width has been greatly narrowed down to a factor of 1.3.

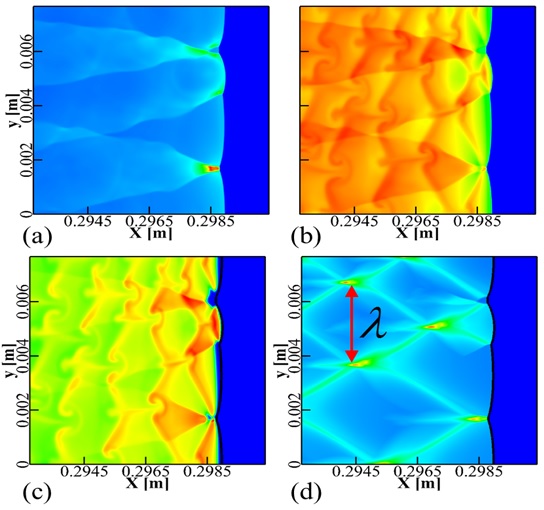
Figure 1. (a) Pressure, (b) temperature, (c) OH field and  (d) numerical soot foil for detonation (stoichiometric H2-O2 diluted with 70% Ar,initial pressure of 0.4 atm, temperature of 300 K)

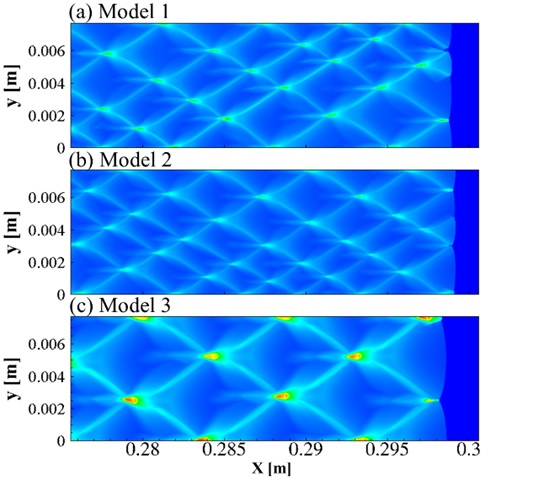
Figure 2. (a) Vibrational equilibrium (b) Vibrational non-equilibrium and (c) Two temperature model (stoichiometric H2-O2 diluted with 70% Ar, initial pressure of 0.4 atm, temperature of 300 K)