# Clear the workspace rm(list=ls()) # Load the libraries we will need library(lme4) # Read the data load( url("http://www.polyu.edu.hk/cbs/sjpolit/data.RData") ) ### MAKING A BARPLOT WITH 95% CIs # Get the means means <- tapply( data$RT, list(data$Condition, data$Tone), mean ) ## Get the 95% CIs using the Cousineau-Morey method (Morey, 2008) # First find the mean for each participant ptpmeans <- aggregate( data$RT, list(data$Subject), mean ) colnames(ptpmeans) <- c("Subject", "Mean") rownames(ptpmeans) <- ptpmeans$Subject # Scale the data by subtracting the participant mean and adding the grand mean data$scaled_RT <- data$RT - ptpmeans[as.character(data$Subject),"Mean"] + mean(data$RT) # The number of conditions K <- length(levels(data$Condition)) + length(levels(data$Tone)) # The number of participants N <- length(levels(data$Subject)) # Get the CIs (using 2 as our estimated t-value, since degrees of freedom for a mixed model are not clear anyway) CIs <- tapply( data$scaled_RT, list( data$Condition, data$Tone), sd ) / sqrt( N-1 ) * 2 * sqrt( K/(K-1) ) ## Done figuring out Cousineau-Morey CIs ## Barplot # Find the ideal y limits ymin <- .9 * ( min(means)-min(CIs) ) ymax <- 1.1 * ( max(means)+max(CIs) ) # Make the barplot xvals <- barplot( means, beside=T, col=c("indianred", "cadetblue"), ylim=c(ymin, ymax), xpd=F ) # Legend legend( "topright", inset=.05, legend=c("Unrelated", "Homogeneous"), fill=c("indianred", "cadetblue") ) # Error bars for confidence intervals arrows( xvals, means-CIs, xvals, means+CIs, angle=90, code=3 ) ## Done with barplot ### DONE PLOTTING
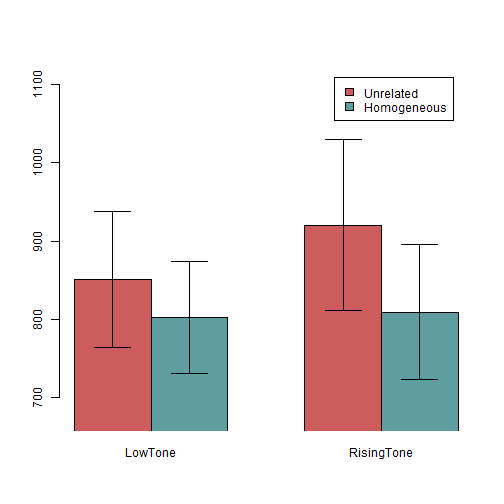
You should notice a clear main effect of Condition (such that Unrelated sets elicited slower responses than Homogeneous sets), and an apparent interaction (such that the effect of Condition is much larger in Rising-Tone than Low-Tone sets). In what follows, we will analyze these data with linear mixed models, using both dummy coding (the default) and deviation coding (the coding scheme which approximates ANOVA results output).
Dummy coding
Calculate a typical linear mixed model using lmer, per the code below. If you are a longtime user of lme4 this
will look very familiar.
dummy_model <- lmer( RT ~ Condition*Tone + (1|Subject) + (1|Item) + (1|List), data )
If you inspect this model (summary(dummy_model)) you will see the following fixed effects in the output:
summary(dummy_model)$coefficients
## Estimate Std. Error t value ## (Intercept) 859.49323 33.14933 25.927918 ## ConditionHomog -61.12232 26.39940 -2.315292 ## ToneRisingTone 68.07547 35.01643 1.944101 ## ConditionHomog:ToneRisingTone -50.30980 36.79587 -1.367267
What do these effects mean? To interpret them, you need to understand what dummy coding is and understand the regression equation (i.e., the general linear model.)
Dummy coding (also called treatment coding) represents the various levels of a factor with 1s and 0s. You can inspect the coding for a factor by running, e.g.,
contrasts(data$Condition) or contrasts(data$Tone). This will give you the following output, letting you know that your variables are dummy-coded:
contrasts(data$Condition)
## Homog ## Unrel 0 ## Homog 1
contrasts(data$Tone)
## RisingTone ## LowTone 0 ## RisingTone 1
Recall that the regression formula for a model like this, which represents the predicted reaction time for a datapoint as a function of that datapoint's associated Condition, Tone, and Condition\(\times\)Tone interaction, is: \(\hat Y_i = b_0 + b_1 X_{1i} + b_2 X_{2i} \ldots + b_n X_{ni}\). In other words, for any given observation \(i\), you start with the Intercept \(b_0\), then add -61.12 (\(b_1)\) times the associated value for Condition (\(X_{1}\)), etc., to reach the predicted value \(\hat Y\) for that observation. Since the value for Condition (\(X_1\)) is either 0 (Unrelated) or 1 (Homogeneous), this amounts to saying that if this datapoint is from the Unrelated condition you add nothing (\(0\times-61.12\)), and if it's from the Homogeneous you subtract 61.12 (\(1\times-61.12\)). The same applies to the effect of Tone. Thus, the Intercept, which is the predicted value for a datapoint for which Condition==Unrelated and Tone==LowTone, corresponds exactly to the predicted value (i.e., the mean, with the additional influence of random effects) for the Unrelated-LowTone condition. The coefficient for Condition.Homog, then, represents how much different the Homogeneous-LowTone condition is from the Intercept (the Unrelated-LowTone condition). Crucially, it should be clear now that this coefficient does not represent a main effect. It represents a simple effect: the effect of Condition within Low Tone sets only. Thus, it would be incorrect to cite this coefficient as evidence for a main effect of Condition; this coefficient only shows the simple effect, not the main effect. As you can see from the bar plot, this simple effect will underestimate the main effect in this dataset (in other datasets it might instead overestimate—for fun, you can look at the barplot and see if you can tell whether the coefficient for Tone in this model will underestimate or overestimate the main effect of Tone). To test a main effect, you need to either conduct model comparison (using e.g. a log-likelihood test), or use deviation coding, described below.
Similarly, for a higher-order design (such as 2\(\times\)2\(\times\)2), then a lower-order interaction term (such as a two-way interaction term) does not represent a true interaction in dummy coding; it represents that interaction at only one level of the third factor. For example, if we added a third factor to the experiment, Lexicality, with words as the baseline level and nonwords as the next level, then a Condition\(\times\)Tone interaction term would not represent a true Condition\(\times\)Tone interaction regardless of Lexicality (like it would in an ANOVA); rather, it would represent the Condition\(\times\)Tone interaction for words only, and not for nonwords. This happens for the same reason that a Condition term (for example) represents only the Condition simple effect for LowTone, rather than a Condition main effect across both Tones. In short, then, if you want to test any effects of a lower order than the highest-order interaction in the design (e.g., if you want to test main effects in a 2\(\times\)2 design, if you want to test main effects or two-way interactions in a 2\(\times\)2\(\times\)2, etc.), then you need to either conduct model comparison or use deviation coding.
Deviation coding
In deviation coding, the contrasts between levels of a [two-level] factor are represented not as 0s and 1s, but as -.5s and .5s. (You may also hear about sum coding or effect coding, which is the same except that it uses -1s and 1s rather than -.5s and .5s; that scheme is sometimes also called deviation coding, which can be confusing.) Thus, there is no longer any one condition that is represented by all 0s; therefore, the Intercept in a model does not represent the baseline condition (like it did in a dummy-coded model), but it now represents the grand mean. For reasons we will see below, this makes deviation coding appropriate for testing main effects of two-level factors.
First, convert the factors from dummy-coded factors to deviation-coded factors. You can do so using the following code:
contrasts(data$Tone) <- rbind(-.5, .5) colnames(contrasts(data$Tone)) <- levels(data$Tone)[2] contrasts(data$Condition) <- rbind(-.5, .5) colnames(contrasts(data$Condition)) <- levels(data$Condition)[2]
Then compute a model using the same regression formula used above:
deviation_model <- lmer( RT ~ Condition*Tone + (1|Subject) + (1|Item) + (1|List), data )
When you inspect this model (summary(deviation_model)) you will see the following fixed effects in the output. Notice that the coefficients
for Intercept, Condition, and Tone are different than the corresponding coefficients in the dummy-coded model.
summary(deviation_model)$coefficients
## Estimate Std. Error t value ## (Intercept) 850.39235 26.61432 31.952431 ## ConditionHomog -86.27722 18.41457 -4.685268 ## ToneRisingTone 42.92057 29.69130 1.445560 ## ConditionHomog:ToneRisingTone -50.30980 36.79587 -1.367267
This model is essentially the same model as that we computed with dummy coding (you can confirm using model comparison, with
anova(deviation_model,dummy_model), that the two models have the exact same fit); the difference is in what the coefficients represent.
Whereas in the dummy-coded model the intercept represented the mean for the baseline condition and the next two coefficients represented
simple effects (the difference between one particular condition and the baseline), in the deviation-coded model the intercept
represents the grand mean (across all conditions) and the coefficients can be interpreted directly as main effects. Specifically, because each
observation of data has a value of either -.5 or .5 for Condition, the coefficient for Condition means that Homogeneous observations are
(\(.5 \times -86.28 = -43.14\)) ms slower than the grand mean, and Unrelated observations are (\(-.5\times-86.28 = 43.14\)) ms slower; by extension
this means that the difference between Homogeneous and Unrelated observations is (\(-43.14 - 43.14 = -86.28\)) ms, exactly that reported in the
model coefficient. The same logic can be used to show that the model coefficient for Tone corresponds to the main effect of Tone.
(Note that these reported main effects will not correspond exactly to the difference in the raw means of the respective conditions—that
is to say, while the model reports a -86.28 main effect of Condition, the difference between the actual means (which can be seen with
tapply(data$RT,data$Condition,mean)) will likely not be this exact value. This is because the model is also accounting for
random effects (repeated measures), which a raw mean is not accounting for. If you calculated a deviation-coded OLS regression with no
random effects (e.g., with a fully between-subjects design where each subject only contributed one observation), the coefficient for Condition should indeed equal the difference between the predicted values for Unrelated and
Homogeneous conditions. As for actually demonstrating that this is the case, I will leave that as a fun exercise for the reader.)
Conclusion
As we have seen above, dummy coding reveals simple effects and deviation coding reveals main effects. Thus, when you interpret (and report) models, especially from a factorial design, it is important to understand the coding scheme you used for categorical predictors. Depending on the situation and the research question of interest, one scheme or another might be more appropriate. For instance, if you want to report mixed-effect model results the same way you would report analysis of variance (ANOVA) results, deviation coding is ideal. On the other hand, dummy coding may be ideal when you are interested in simple effects. For example, a useful trick is to use dummy-coded factors that are nested, rather than crossed, in which case the model coefficients will give the simple effect of the nested factor at each level of the nesting factor; the following code, for instance, will return coefficients giving the Condition effect for each tone:
# Convert Tone back to dummy coding contrasts(data$Tone) <- rbind(0, 1) colnames(contrasts(data$Tone)) <- levels(data$Tone)[2] # Convert Condition back to dummy coding contrasts(data$Condition) <- rbind(0, 1) colnames(contrasts(data$Condition)) <- levels(data$Condition)[2] # Calculate a nested model nested_dummy_model <- lmer( RT ~ Tone/Condition + (1|Subject) + (1|Item) + (1|List), data )
After confirming that this model has the exact same fit as the other models (anova(dummy_model,nested_dummy_model)),
you can inspect the model to see that it gives a separate Condition coefficient for each level of Tone. (This model doesn't provide any coefficient
that directly reports and tests the significance of the interaction, though; with this coding scheme, the interaction must be tested with model comparison.
This is in fact the exact scheme I used to analyze and report these data in Politzer-Ahles & Zhang, in press, as well as
similar data in Politzer-Ahles & Fiorentino, 2013.)
summary(nested_dummy_model)$coefficients
## Estimate Std. Error t value ## (Intercept) 859.49323 33.14933 25.927918 ## ToneRisingTone 68.07547 35.01643 1.944101 ## ToneLowTone:ConditionHomog -61.12232 26.39940 -2.315292 ## ToneRisingTone:ConditionHomog -111.43211 25.65605 -4.343307
Finally, note that this example used the simplest possible factorial design, 2\(\times\)2. The presentation and interpretation of model coefficients will be more complicated than this if the design includes any polytomous factors (i.e., factors with more than two levels). See the links provided at the top of this article for more detailed discussion, including examples, of how these coding schemes work in such designs. For polytomous factors, most of the discussion above is moot, since once you include a polytomous factor in your design then you have left the world of making broad claims about main effects and interactions via model coefficients (since any such main effects and interactions will have multiple coefficients associated with them) and entered the world where model comparison is necessary.
by Stephen Politzer-Ahles. Last modified on 2015-12-22.